A diagramless crossword puzzle is similar to an American-style crossword puzzle and follows all the same rules. However the locations of the clue numbers and shaded (black) squares are unspecified. Essentially, you're provided only a blank grid along with the crossword clues.
A human solver must deduce two things:
This builder tackles ONLY the second part - it builds the entire crossword grid without considering the clues or the clue answers whatsoever. It will soley look at the clue numbers and whether they are an across clue, a down clue, or both.
Diagramless crossword puzzles also tend to give some hints, which can be added here as parameters. These include symmetry (and the different types thereof) and where is the 'starting square' of the puzzle. This program can take these inputs, and return all possible solutions for the given puzzle.
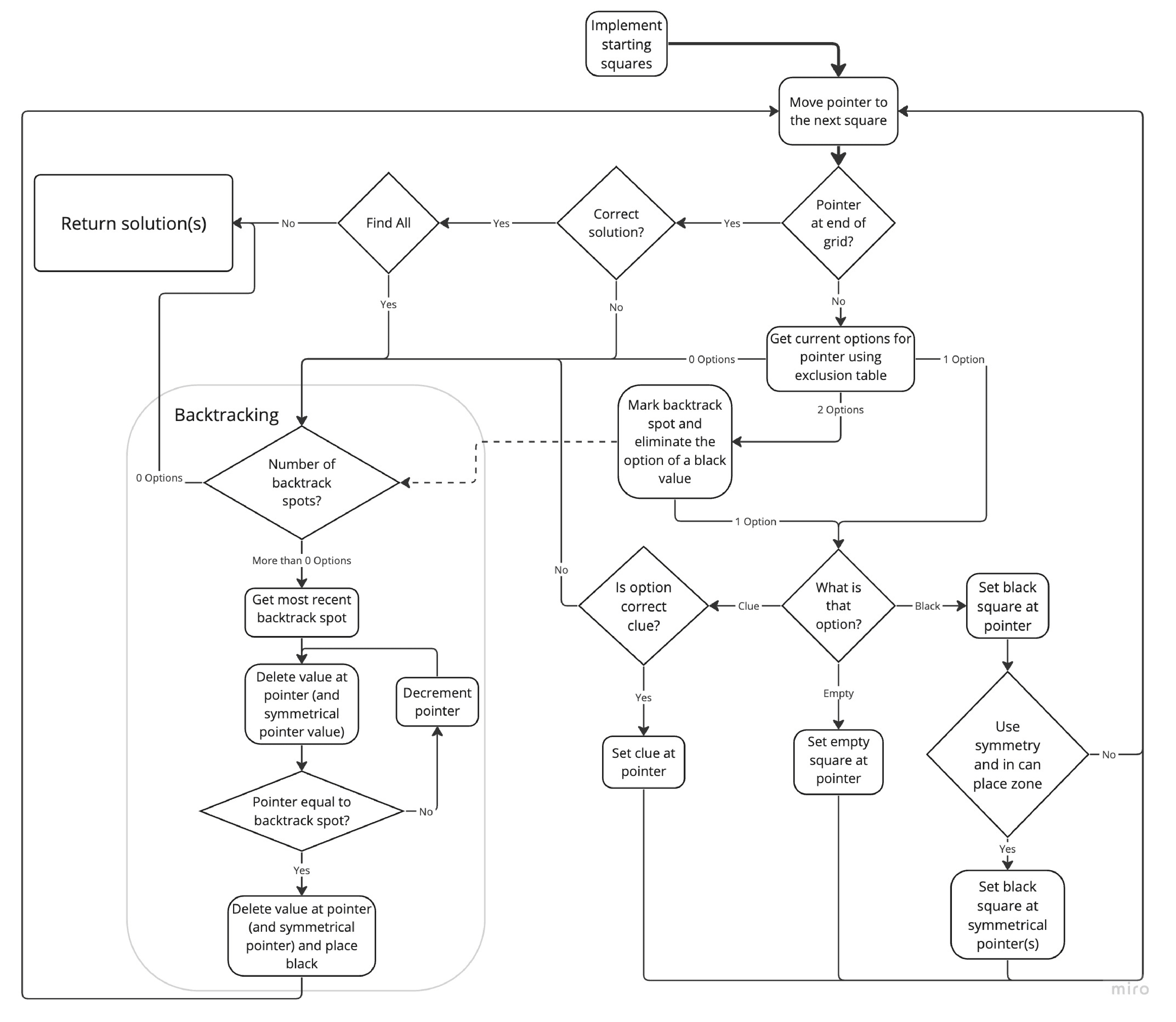
At a basic level, the program through each square, placing the correct value, as determined by the exclusion table.
If there are two possible values, the options will always be a black square or some other value. At this point the solver will mark a backtracking point, and continue on solving with the other value. This will proceed until there are no possible options (at which point it will backtrack) or the puzzle is correct.
The basic psuedocode is outlined below and a visual representation can be found further down:
If the puzzle is searching for every solution, it will exit this loop only when there are no more backtracking spots. Otherwise it will exit after the first solution.
The exclusion table is used to help determine which values are possible for a single square. It analyzes each of the square's neighbors, one at a time, and determines what is NOT possible for that specific configuration. For example, if direcly above the pointer there is a black square, then it is impossible for the pointer to be either an across clue or an empty square, based on the rules of crossword puzzles.
A point to note, this exclusion table ONLY looks at the pointer and that specific neighbor, one at a time. So if Up 2 is black, it does not check what up 1 is when determining what is 'impossble'. Because of this, some of the values in this lookup table are empty, meaning that that configuration does not restrict the pointer's possible values.
The algorithm continues through every one of the possible influential pointer neighbors (Up 1, Up 2, Up 3, Down 1, Down 2, Down 3, Left 1, Left 2, Left 3, Right 1, Right 2, Right 3), building a set of impossible values for that square.
Some other restrictions are added to the square at this point:
Then the difference between these impossible values and all values results in only the possible values left.
The exclusion table is a bit of a misnomer, as it is actually a dictionary, but this was just done to decrease time complexity.
When symmetry is enforced, it tends to speed up the process signficantly. For each black square placed, the solver will be able to place one (or more) symmetrical black squares.
So in order to speed up the process during solving, for each type of symmetry we need to determine two different 'zones', one where we place black squares and one where ONLY symmetrically mirrored black squares are placed based on the first zone. If the pointer is in the 'can place' zone, then it will place a black square in that zone, and the corresponding black squares in the symetrical location(s).
This solver allows for a few different kinds of symmetry, laid out here:
| Type | Explanation |
|---|---|
| Rotational | Also known as Standard Crossword Symmetry or 180˚ Rotational Symmetry, every square has a counterpart by spinning a half turn about the puzzle's center point. |
| Left Right | Also known as Mirror Symmetry, every square has a counterpart across the puzzle's vertical axis. |
| Up Down | Every square has a counterpart across the puzzle's horizontal axis. |
| Diagonal - Top Left Start | Every square has a counterpart across the puzzle's diagonal axis, from the top left to the bottom right. |
| Diagonal - Top Right Start | Every square has a counterpart across the puzzle's diagonal axis, from the top right to the bottom left. |
| Dual Rotational | Building on Rotational Symmetry, every square has counterparts by spinning a quarter turn, a half turn, and a three quarter turn about the puzzle's center point. |
| Three Way | Combines Left Right, Up Down and Rotational Symmetries. With the exception of the center row and column, every square has three symmetrical counterparts. |
| Super | Combines Left Right, Up Down, Rotational, Dual Rotational and both Diagonal Symmetries. |
| Asymmetry | No Symmetry. |
Github for the original Python version run from the terminal.
Github for the Web / Python version seen here.
This is still a work in progress so please reach out if you have any questions, comments, or suggestions!
Jordan Karp - jordanmatthew.karp@gmail.com